Flux Form Of Green's Theorem
Flux Form Of Green's Theorem - Formal definition of divergence what we're building to the 2d divergence theorem is to divergence what green's theorem is to curl. Web flux form of green's theorem. Start with the left side of green's theorem: A circulation form and a flux form, both of which require region d in the double integral to be simply connected. Let r r be the region enclosed by c c. 27k views 11 years ago line integrals. Tangential form normal form work by f flux of f source rate around c across c for r 3. Green’s theorem comes in two forms: The discussion is given in terms of velocity fields of fluid flows (a fluid is a liquid or a gas) because they are easy to visualize. This can also be written compactly in vector form as (2)
A circulation form and a flux form, both of which require region d in the double integral to be simply connected. Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y − q d x = ∬ r ∇ ⋅ f → d a if f =[p q] f → = [ p q] (omitting other hypotheses of course). Over a region in the plane with boundary , green's theorem states (1) where the left side is a line integral and the right side is a surface integral. Web green’s theorem is a version of the fundamental theorem of calculus in one higher dimension. Web green's theorem is a vector identity which is equivalent to the curl theorem in the plane. In the circulation form, the integrand is f⋅t f ⋅ t. Tangential form normal form work by f flux of f source rate around c across c for r 3. All four of these have very similar intuitions. Web 11 years ago exactly. Green’s theorem has two forms:
The function curl f can be thought of as measuring the rotational tendency of. Formal definition of divergence what we're building to the 2d divergence theorem is to divergence what green's theorem is to curl. Then we will study the line integral for flux of a field across a curve. 27k views 11 years ago line integrals. Because this form of green’s theorem contains unit normal vector n n, it is sometimes referred to as the normal form of green’s theorem. Web green's theorem is most commonly presented like this: The discussion is given in terms of velocity fields of fluid flows (a fluid is a liquid or a gas) because they are easy to visualize. Web green’s theorem states that ∮ c f → ⋅ d r → = ∬ r curl f → d a; Web first we will give green’s theorem in work form. A circulation form and a flux form.
Flux Form of Green's Theorem YouTube
Then we will study the line integral for flux of a field across a curve. Web green’s theorem states that ∮ c f → ⋅ d r → = ∬ r curl f → d a; Since curl f → = 0 in this example, the double integral is simply 0 and hence the circulation.
Green's Theorem YouTube
Green's theorem allows us to convert the line integral into a double integral over the region enclosed by c. An interpretation for curl f. Web circulation form of green's theorem google classroom assume that c c is a positively oriented, piecewise smooth, simple, closed curve. All four of these have very similar intuitions. It relates the line integral of a.
Flux Form of Green's Theorem Vector Calculus YouTube
A circulation form and a flux form, both of which require region d in the double integral to be simply connected. Web the flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). Finally we will give green’s theorem in. Green's theorem 2d divergence theorem stokes' theorem 3d divergence theorem here's the.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Parabola
Formal definition of divergence what we're building to the 2d divergence theorem is to divergence what green's theorem is to curl. All four of these have very similar intuitions. Start with the left side of green's theorem: Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the.
multivariable calculus How are the two forms of Green's theorem are
This can also be written compactly in vector form as (2) The discussion is given in terms of velocity fields of fluid flows (a fluid is a liquid or a gas) because they are easy to visualize. Green's theorem allows us to convert the line integral into a double integral over the region enclosed by c. Its the same convention.
Green's Theorem Flux Form YouTube
Web 11 years ago exactly. Proof recall that ∮ f⋅nds = ∮c−qdx+p dy ∮ f ⋅ n d s = ∮ c − q d x + p d y. Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the theorem is a shortcut for line integrals.
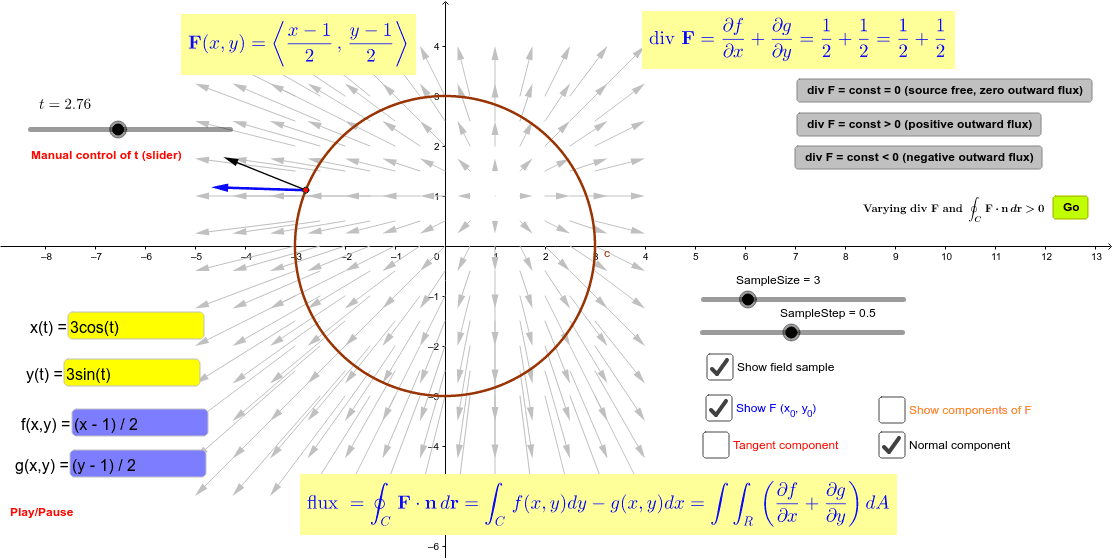
Illustration of the flux form of the Green's Theorem GeoGebra
Green’s theorem comes in two forms: It relates the line integral of a vector field around a planecurve to a double integral of “the derivative” of the vector field in the interiorof the curve. Green's theorem 2d divergence theorem stokes' theorem 3d divergence theorem here's the good news: Green's theorem allows us to convert the line integral into a double.
Calculus 3 Sec. 17.4 Part 2 Green's Theorem, Flux YouTube
Web green's theorem is one of four major theorems at the culmination of multivariable calculus: Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y − q d x = ∬ r ∇.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Hole
Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus: Using green's theorem in its circulation and flux forms, determine the flux and circulation of f around the triangle t, where t is the triangle with vertices ( 0, 0), ( 1, 0), and ( 0, 1), oriented counterclockwise. A circulation.
Determine the Flux of a 2D Vector Field Using Green's Theorem
Green's, stokes', and the divergence theorems 600 possible mastery points about this unit here we cover four different ways to extend the fundamental theorem of calculus to multiple dimensions. Web the flux form of green’s theorem relates a double integral over region d d to the flux across curve c c. However, green's theorem applies to any vector field, independent.
Then We State The Flux Form.
Web using green's theorem to find the flux. Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the theorem is a shortcut for line integrals when the curve is a boundary. Web green’s theorem states that ∮ c f → ⋅ d r → = ∬ r curl f → d a; Over a region in the plane with boundary , green's theorem states (1) where the left side is a line integral and the right side is a surface integral.
Web 11 Years Ago Exactly.
Web in this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. For our f f →, we have ∇ ⋅f = 0 ∇ ⋅ f → = 0. An interpretation for curl f. Finally we will give green’s theorem in.
Start With The Left Side Of Green's Theorem:
Let r r be the region enclosed by c c. Then we will study the line integral for flux of a field across a curve. In the circulation form, the integrand is f⋅t f ⋅ t. 27k views 11 years ago line integrals.
Web Flux Form Of Green's Theorem.
In this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Because this form of green’s theorem contains unit normal vector n n, it is sometimes referred to as the normal form of green’s theorem. Green's, stokes', and the divergence theorems 600 possible mastery points about this unit here we cover four different ways to extend the fundamental theorem of calculus to multiple dimensions. Note that r r is the region bounded by the curve c c.