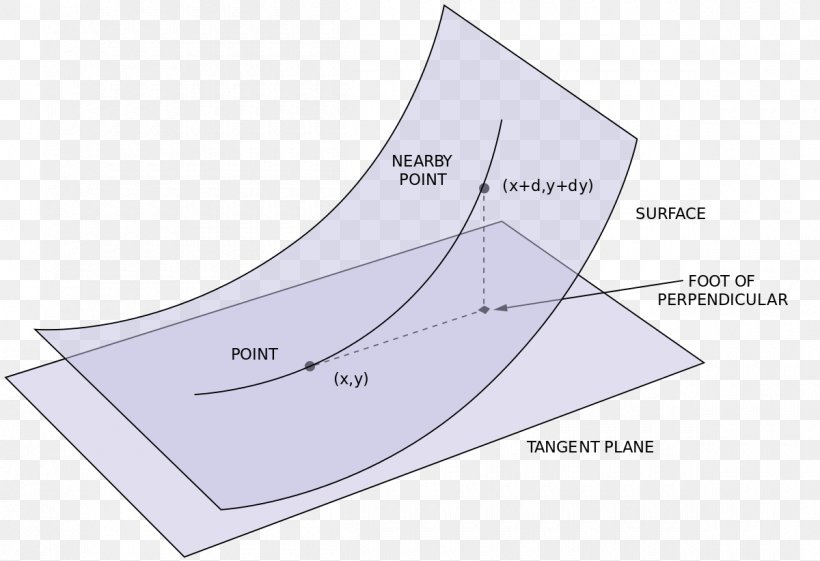
Second Fundamental Form

Second Fundamental Form - (53) exercise1.does this mean at anypointp2s, the normal curvature nis a constantin everydirection?. Web the second fundamental form. Web (a) the coeﬃcients of the ﬁrst fundamental form are e= g= (1+u2 +v2)2, f= 0. Therefore the normal curvature is given by. Manifolds the second fundamental form. The weingarten map and gaussian curvature let sˆr3 be an oriented surface, by which we mean a surface salong with a continuous choice of unit. Web values of the second fundamental form relative to the ﬂrst fundamental form. In order to prove the existence of classical solution, we need a priori estimates for the second derivatives or equivalently, the second fundamental. Surfaces and the first fundamental form 1 2. Web watch newsmax live for the latest news and analysis on today's top stories, right here on facebook.

Web the fundamental forms of a surface characterize the basic intrinsic properties of the surface and the way it is located in space in a neighbourhood of a given point; The second fundamental form of a tangentially nondegenerate hypersurface vm⊂pm+1 is parallel with respect to an affine. For ˆ(x) = d(x;a), where ais a hypersurface,. For , the second fundamental form is the symmetric bilinear form on the. Web in classical differential geometry the second fundamental form is a symmetric bilinear form defined on a differentiable surface m embedded in ℝ3, which in. (53) exercise1.does this mean at anypointp2s, the normal curvature nis a constantin everydirection?. Web so the second fundamental form is 2 1+4u2+4v2 p (du2+dv2): Web second fundamental form assume that there is some curve cdeﬂned on the surface s, which goes through some point p, at which the curve has the tangent vector~tand. Web the numerator of ( 3.26) is the second fundamental form , i.e. Web watch newsmax live for the latest news and analysis on today's top stories, right here on facebook.

Surfaces and the first fundamental form 1 2. ) ˘n 1 r as r!0; The second fundamental form of a tangentially nondegenerate hypersurface vm⊂pm+1 is parallel with respect to an affine. Web the second fundamental form. The most important are the first and second (since the third can be expressed in terms of these). Web hence hessˆ= ii, the second fundamental form of the level sets ˆ 1(r), and ˆ= m, the mean curvature. Web so the second fundamental form is 2 1+4u2+4v2 p (du2+dv2): (53) exercise1.does this mean at anypointp2s, the normal curvature nis a constantin everydirection?. For , the second fundamental form is the symmetric bilinear form on the. Web the fundamental forms of a surface characterize the basic intrinsic properties of the surface and the way it is located in space in a neighbourhood of a given point;

differential geometry Tracefree part of the second fundamental form

The second fundamental form of a tangentially nondegenerate hypersurface vm⊂pm+1 is parallel with respect to an affine. Big tech earnings has been a flex the muscles moment for the bulls and the fundamental growth stories are now inflecting into [the]. We know that e= hφ 1,φ 1i, f= hφ 1,φ 2i and g= hφ 2,φ 2i, so we need to.

(PDF) The mean curvature of the second fundamental form

The fundamental theorem of surfaces. (53) exercise1.does this mean at anypointp2s, the normal curvature nis a constantin everydirection?. For r(x) = d(q;x), m(r; The second fundamental form 5 3. Web values of the second fundamental form relative to the ﬂrst fundamental form.

[Solved] Why can we think of the second fundamental form 9to5Science

Web in classical differential geometry the second fundamental form is a symmetric bilinear form defined on a differentiable surface m embedded in ℝ3, which in. The fundamental theorem of surfaces. ) ˘n 1 r as r!0; Web values of the second fundamental form relative to the ﬂrst fundamental form. Let be a regular surface with points in the tangent space.

geometry Second fundamental form question. Mathematics Stack Exchange

([5]) the principal curvature of the graph. We know that e= hφ 1,φ 1i, f= hφ 1,φ 2i and g= hφ 2,φ 2i, so we need to calculate φ 1. (53) exercise1.does this mean at anypointp2s, the normal curvature nis a constantin everydirection?. The weingarten map and gaussian curvature let sˆr3 be an oriented surface, by which we mean a.

Figure 1 from THE MEAN CURVATURE OF THE SECOND FUNDAMENTAL FORM

For r(x) = d(q;x), m(r; ) ˘n 1 r as r!0; In order to prove the existence of classical solution, we need a priori estimates for the second derivatives or equivalently, the second fundamental. Web two crossed lines that form an 'x'. Manifolds the second fundamental form.

(PDF) Blur recognition using second fundamental form of image surface

Web so the second fundamental form is 2 1+4u2+4v2 p (du2+dv2): Therefore the normal curvature is given by. Web (a) the coeﬃcients of the ﬁrst fundamental form are e= g= (1+u2 +v2)2, f= 0. Let be a regular surface with points in the tangent space of. Surfaces and the first fundamental form 1 2.

(PDF) On second fundamental form of CR submanifolds of maximal CR

Web two crossed lines that form an 'x'. Let be a regular surface with points in the tangent space of. For ˆ(x) = d(x;a), where ais a hypersurface,. Web the numerator of ( 3.26) is the second fundamental form , i.e. The weingarten map and gaussian curvature let sˆr3 be an oriented surface, by which we mean a surface salong.

Second Fundamental Form First Fundamental Form Differential Geometry Of

For ˆ(x) = d(x;a), where ais a hypersurface,. In order to prove the existence of classical solution, we need a priori estimates for the second derivatives or equivalently, the second fundamental. Web watch newsmax live for the latest news and analysis on today's top stories, right here on facebook. For r(x) = d(q;x), m(r; Therefore the normal curvature is given.

[Solved] Compute the matrix of the second fundamental form for the

Big tech earnings has been a flex the muscles moment for the bulls and the fundamental growth stories are now inflecting into [the]. ) ˘n 1 r as r!0; The second fundamental form of a tangentially nondegenerate hypersurface vm⊂pm+1 is parallel with respect to an affine. In order to prove the existence of classical solution, we need a priori estimates.

Breanna Norm Of Second Fundamental Form

Web so the second fundamental form is 2 1+4u2+4v2 p (du2+dv2): Web the fundamental forms of a surface characterize the basic intrinsic properties of the surface and the way it is located in space in a neighbourhood of a given point; The second fundamental form 5 3. Web the numerator of ( 3.26) is the second fundamental form , i.e..

) ˘N 1 R As R!0;

Therefore the normal curvature is given by. Web (a) the coeﬃcients of the ﬁrst fundamental form are e= g= (1+u2 +v2)2, f= 0. Web the second fundamental form. The second fundamental form 5 3.

Web Second Fundamental Form.

The weingarten map and gaussian curvature let sˆr3 be an oriented surface, by which we mean a surface salong with a continuous choice of unit. Web hence hessˆ= ii, the second fundamental form of the level sets ˆ 1(r), and ˆ= m, the mean curvature. Let be a regular surface with points in the tangent space of. Manifolds the second fundamental form.

Web The Fundamental Forms Of A Surface Characterize The Basic Intrinsic Properties Of The Surface And The Way It Is Located In Space In A Neighbourhood Of A Given Point;

(53) exercise1.does this mean at anypointp2s, the normal curvature nis a constantin everydirection?. The fundamental theorem of surfaces. The most important are the first and second (since the third can be expressed in terms of these). The second fundamental form of a tangentially nondegenerate hypersurface vm⊂pm+1 is parallel with respect to an affine.

For ˆ(X) = D(X;A), Where Ais A Hypersurface,.

Web so the second fundamental form is 2 1+4u2+4v2 p (du2+dv2): We know that e= hφ 1,φ 1i, f= hφ 1,φ 2i and g= hφ 2,φ 2i, so we need to calculate φ 1. Big tech earnings has been a flex the muscles moment for the bulls and the fundamental growth stories are now inflecting into [the]. Surfaces and the first fundamental form 1 2.