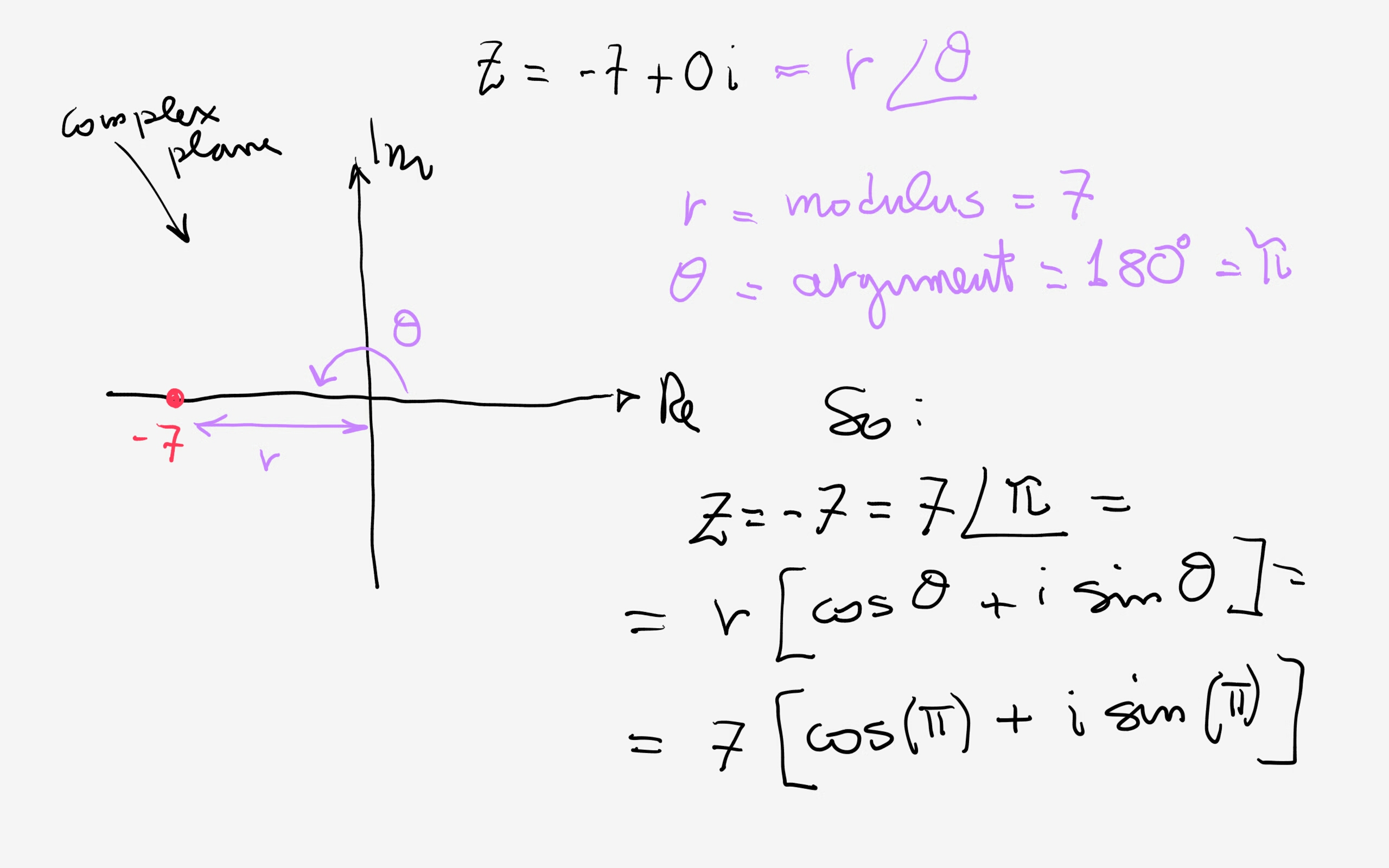Trigonometric Form Of A Vector

Trigonometric Form Of A Vector - Or if you had a vector of magnitude one, it would be cosine of that angle, would be the x component, for the, if we had a unit vector there in that direction. Component form in component form, we treat the vector as a point on the coordinate plane, or as a directed line segment on the plane. Summation of trigonometric form clarity and properties; Right triangles & trigonometry sine and cosine of complementary angles: 2.1.2 perform basic vector operations (scalar multiplication, addition, subtraction).; The direction of a vector is only fixed when that vector is viewed in the coordinate plane. $$v_x = \lvert \overset{\rightharpoonup}{v} \rvert \cos θ$$ $$v_y = \lvert \overset{\rightharpoonup}{v} \rvert \sin θ$$ $$\lvert \overset{\rightharpoonup}{v} \rvert = \sqrt{v_x^2 + v_y^2}$$ $$\tan θ = \frac{v_y}{v_x}$$ In the above figure, the components can be quickly read. Web the sum of two vectors is known as the resultant, and you can use trigonometry to help you find it. Plug the solutions into the definition of.

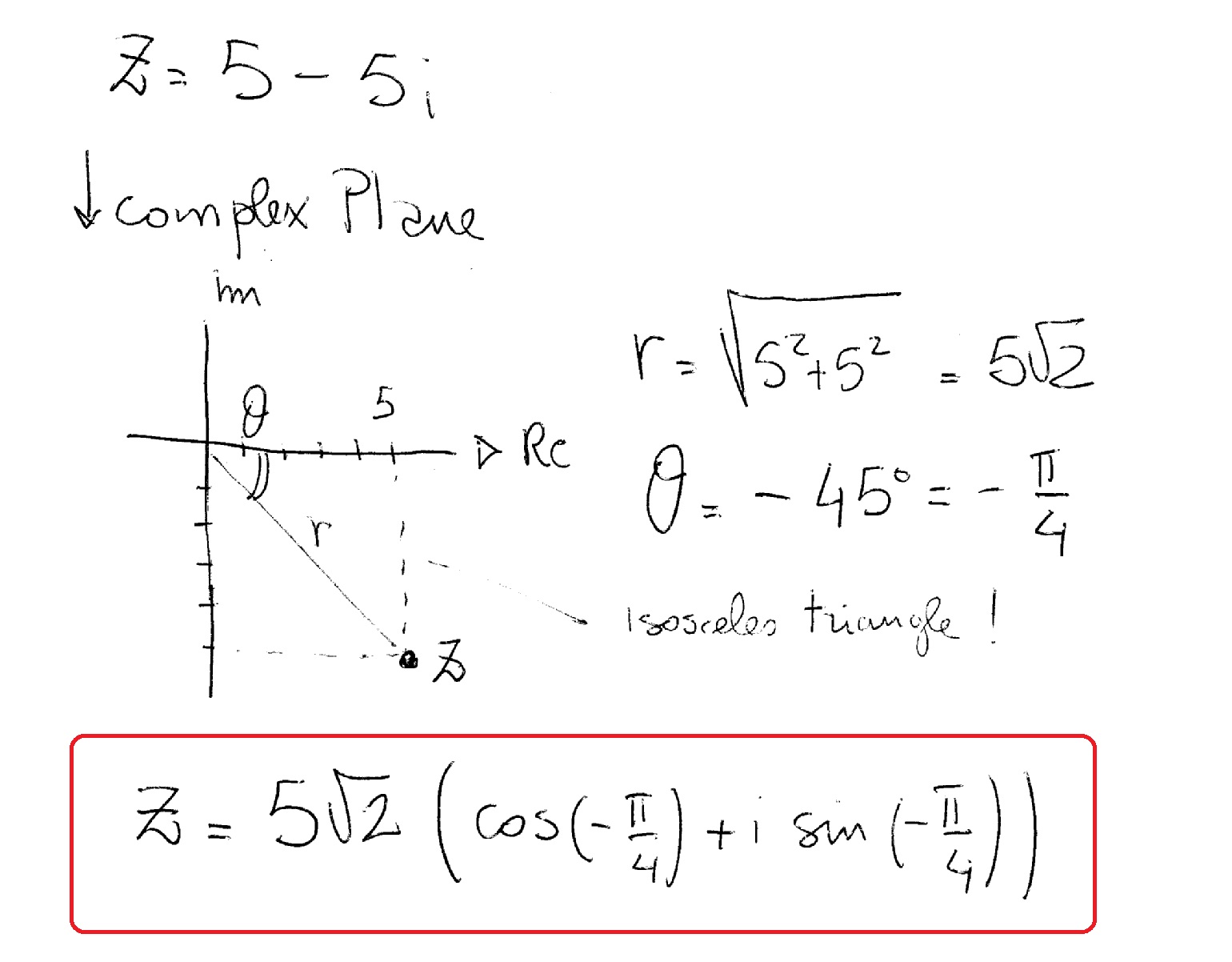
Web z = r(cos(θ) + isin(θ)). Z = a+ bi = |z|(cos(θ)+isin(θ)) z = a + b i = | z | ( cos ( θ) + i sin ( θ)) 2.1.4 explain the formula for the magnitude of a vector.; Add in the triangle legs. The direction of a vector is only fixed when that vector is viewed in the coordinate plane. Right triangles & trigonometry sine and cosine of complementary angles: Web to find the direction of a vector from its components, we take the inverse tangent of the ratio of the components: Two vectors are shown below: 2.1.2 perform basic vector operations (scalar multiplication, addition, subtraction).; ˆu = < 2,5 >.

We will also be using these vectors in our example later. 2.1.5 express a vector in terms of unit vectors.; The trigonometric ratios give the relation between magnitude of the vector and the components of the vector. −→ oa = ˆu = (2ˆi +5ˆj) in component form. Cosine is the x coordinate of where you intersected the unit circle, and sine is the y coordinate. The angle θ is called the argument of the argument of the complex number z and the real number r is the modulus or norm of z. 2.1.6 give two examples of vector quantities. Web when finding the magnitude of the vector, you use either the pythagorean theorem by forming a right triangle with the vector in question or you can use the distance formula. Want to learn more about vector component form? Or if you had a vector of magnitude one, it would be cosine of that angle, would be the x component, for the, if we had a unit vector there in that direction.

Trigonometric Form To Standard Form

Web the sum of two vectors is known as the resultant, and you can use trigonometry to help you find it. 2.1.6 give two examples of vector quantities. How to write a component. The length of the arrow (relative to some kind of reference or scale) represents the relative magnitude of the vector while the arrow head gives. −→ oa.

The Product and Quotient of Complex Numbers in Trigonometric Form YouTube

Web the length of a vector is formally called its magnitude. Web the sum of two vectors $\vec{u}$ and $\vec{v}$, or vector addition, produces a third vector $\overrightarrow{u+ v}$, the resultant vector. Web how to write a component form vector in trigonometric form (using the magnitude and direction angle). Want to learn more about vector component form? Right triangles &.

18+ trigonometric form of a vector KhailaMillen

The vector in the component form is v → = 〈 4 , 5 〉. And then sine would be the y component. 2.1.3 express a vector in component form.; Web in trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined..

Trigonometric Form To Standard Form

To find $\overrightarrow{u + v}$, we first draw the vector $\vec{u}$, and from the terminal end of $\vec{u}$, we drawn the vector $\vec{v}$. Summation of trigonometric form clarity and properties; Two vectors are shown below: Web the vector and its components form a right triangle. $$v_x = \lvert \overset{\rightharpoonup}{v} \rvert \cos θ$$ $$v_y = \lvert \overset{\rightharpoonup}{v} \rvert \sin θ$$ $$\lvert.

Vector Components Trigonometry Formula Sheet Math words, Math quotes

Using trigonometry the following relationships are revealed. 2.1.3 express a vector in component form.; 2.1.6 give two examples of vector quantities. To find $\overrightarrow{u + v}$, we first draw the vector $\vec{u}$, and from the terminal end of $\vec{u}$, we drawn the vector $\vec{v}$. The trigonometric ratios give the relation between magnitude of the vector and the components of the.

Trig Form of a Vector YouTube

2.1.3 express a vector in component form.; Plug the solutions into the definition of. Web a vector is defined as a quantity with both magnitude and direction. Web what lives trigonometry form? Right triangles & trigonometry sine and cosine of complementary angles:

Vectors in Trigonmetric Form YouTube

To find $\overrightarrow{u + v}$, we first draw the vector $\vec{u}$, and from the terminal end of $\vec{u}$, we drawn the vector $\vec{v}$. Web a vector [math processing error] can be represented as a pointed arrow drawn in space: Magnitude & direction form of vectors. We will also be using these vectors in our example later. Right triangles & trigonometry.

Trigonometric Form To Polar Form

Web the sum of two vectors $\vec{u}$ and $\vec{v}$, or vector addition, produces a third vector $\overrightarrow{u+ v}$, the resultant vector. Web the sum of two vectors is known as the resultant, and you can use trigonometry to help you find it. 2.1.2 perform basic vector operations (scalar multiplication, addition, subtraction).; Right triangles & trigonometry the reciprocal trigonometric ratios: Web.

Trigonometric chart Cuemath

Web a vector [math processing error] can be represented as a pointed arrow drawn in space: Component form in component form, we treat the vector as a point on the coordinate plane, or as a directed line segment on the plane. To find $\overrightarrow{u + v}$, we first draw the vector $\vec{u}$, and from the terminal end of $\vec{u}$, we.

PPT Introduction to Biomechanics and Vector Resolution PowerPoint

Web a vector is defined as a quantity with both magnitude and direction. Z = a+ bi = |z|(cos(θ)+isin(θ)) z = a + b i = | z | ( cos ( θ) + i sin ( θ)) Add in the triangle legs. Adding vectors in magnitude & direction form. −→ oa and −→ ob.

$$V_X = \Lvert \Overset{\Rightharpoonup}{V} \Rvert \Cos Θ$$ $$V_Y = \Lvert \Overset{\Rightharpoonup}{V} \Rvert \Sin Θ$$ $$\Lvert \Overset{\Rightharpoonup}{V} \Rvert = \Sqrt{V_X^2 + V_Y^2}$$ $$\Tan Θ = \Frac{V_Y}{V_X}$$

2.1.3 express a vector in component form.; The vector in the component form is v → = 〈 4 , 5 〉. The trigonometric ratios give the relation between magnitude of the vector and the components of the vector. 2.1.1 describe a plane vector, using correct notation.;

Two Vectors Are Shown Below:

Summation of trigonometric form clarity and properties; Web a vector [math processing error] can be represented as a pointed arrow drawn in space: Magnitude & direction form of vectors. Web how to write a component form vector in trigonometric form (using the magnitude and direction angle).

−→ Oa = ˆU = (2ˆI +5ˆJ) In Component Form.

Web in trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Web draw the vector. Or if you had a vector of magnitude one, it would be cosine of that angle, would be the x component, for the, if we had a unit vector there in that direction. Web solving for an angle in a right triangle using the trigonometric ratios:

Add In The Triangle Legs.

Web to find the direction of a vector from its components, we take the inverse tangent of the ratio of the components: Cosine is the x coordinate of where you intersected the unit circle, and sine is the y coordinate. How to write a component. Web what lives trigonometry form?